Es indudable la bondad del modelo para Bogotá. Es más completo que los otros y permite por medio de cambiar el valor de los parámetros hacer ajustes a medida que se va avanzando en el tiempo. Es decir, es relativamente fácil actualizarlo. Se incluyó el modelo SIR dado su carácter de pionero y precisamente el modelo de Bogotá es una variante con la misma filosofía. En la literatura sobre el tema hay modelos donde se incluye adicionalmente ecuaciones que recogen la dinámica de nacimientos y defunciones por otras causas u otras variables. Sin embargo, en la mayoría de casos se trata de esquemas de compartimentos.
Por Diego Escobar
Economista y matemático
Economista y matemático
Este
documento tiene tres partes. En la primera, se van a usar las bases de datos
del Ministerio de Salud para Colombia y de la Alcaldía Mayor de Bogotá para la
ciudad. El carácter de esta primera parte es de tipo descriptivo y nos
familiariza con términos y conceptos que esclarecen el tema. En la segunda
parte, se van a presentar algunos modelos matemáticos para poder ver la
evolución de las variables claves de la pandemia. En la última parte, se hará
mención de otros modelos que se han venido utilizando y publicando en todo el
mundo. No se pretende ser exhaustivo debido a que hoy por hoy la literatura es
extensa.
Análisis descriptivo
En
el gráfico No. 1 se muestra el total de infectados para todo el país, para
Bogotá y para el Resto del país excluyendo Bogotá[1].
No
se percibe, por un lado, el ‘aplanamiento’ de las curvas y, por el otro, las
tasas de crecimiento[2]
para diferentes períodos muestran el siguiente panorama:
Cuadro 1: Tasas de crecimiento
Es
decir, el crecimiento promedio diario es menor para todo el país a partir de la
cuarentena del 25 de marzo. Se reduce aún más a partir del 14 de abril y para
el corto periodo desde la última prórroga, donde Bogotá alcanza un 3.49%. En
cambio el del grupo Resto es mayor a causa de los casos de Villavicencio y
Leticia.
Observando
la gráfica que muestra promedios móviles con amplitud de 3 y 7 días tampoco se
detecta el aplanamiento.
Gráfico 2: Medias móviles
Con
respecto a los infectados según si se trata de casos importados o relacionados
(contacto entre personas ya en el país) el panorama se presenta de la siguiente
forma:
Gráfico 3: Infectados por Tipo
Observando
en el caso de los importados por países y regiones, el panorama muestra los
siguientes resultados:
Cuadro 2: Origen de los
infectados
Se
aplanó la curva de los casos importados, pero no en forma inmediata con el
cierre de aeropuertos (25 de marzo) sino un poco después. En parte esto
corresponde a los casos que se muestran en el cuadro donde se detecta que para
Ecuador, Brasil y Panamá – países fronterizos de Colombia – un 62%. 83% y 85%,
respectivamente, son después del cierre de aeropuertos.
Para
finalizar esta parte descriptiva se muestra, por un lado, la evolución de los
casos infectados desde el punto de vista del número de días en que se duplican
estos:
Cuadro 3: No. De días en que
se duplican los infectados
Los
datos muestran que al inicio los días en que se duplicaban los infectados era
muy rápido y ya para el último dato de que se dispone toma 14 días en pasar de
3584 casos a 7196.
Para
el caso de Bogotá se utiliza la base de datos https://bogota.gov.co/coronavirus-en-bogota/[3] que
también usaremos posteriormente para el modelo del COVID-19 para la ciudad.
Los
dos gráficos que siguen muestran la evolución en el tiempo (6 de marzo-23
abril) del total de casos y además distinguiendo entre los infectados los casos
moderados, críticos y severos además de los fallecidos.
Gráfico 4: Infectados
Se
deduce un crecimiento fuerte de los casos severos, que se estabilizan al final
del periodo de observación, que pueden convertirse en críticos y en los
moderados que pueden convertirse en críticos y necesiten pasar a UCI o ser
hospitalizados, respectivamente y, un crecimiento en el número de fallecidos –
130 a 5 de mayo – pero con varios días en que no hubo nuevos casos.
Con
respecto al tiempo de duplicación para el caso de Bogotá el panorama es similar
al de todo el país.
Cuadro 4: Duplicación en
Bogotá
Finalmente,
una nota sobre el número de casos por localidad y la tasa de crecimiento de
éstas para el período de dos meses entre marzo 6 y mayo 53:
Cuadro 5: Infectados por
localidad y tasa de crecimiento
Los
datos muestran 9 localidades con un crecimiento superior al 10% siendo
preocupante los casos de Bosa, San Cristóbal y Kennedy.
Modelamiento matemático del
covid-19
Existen
multiplicidad de publicaciones de muchos modelos matemáticos en todo el mundo
que tratan de explicar el comportamiento del virus, hacer proyecciones y servir
como un instrumento para ayudar a tomar decisiones acertadas. George Box un
conocido estadístico británico decía en 1976: “En esencia, todos los modelos están equivocados,
pero algunos son útiles".
En esta parte del documento vamos a tratar tres modelos que,
por un lado son sencillos, pero que tienen mucha difusión.
El modelo de Gompertz
El
británico Benjamin Gompertz desarrolló en 1825 la ley que se conoce como ‘mortalidad
de Gompertz’ que afirma que si la población en el tiempo t es P(t) (función de
Gompertz) y c es la tasa de crecimiento y K el número de individuos en
equilibrio (se conoce también como capacidad de carga) entonces como resultado
de una ecuación diferencial con valor inicial Po se tiene que:
En
la ciencia actuarial la ley de Gompertz es fundamental para la construcción de
tablas de mortalidad que utilizan las compañías de seguros para sus cálculos de
primas y rentas.
Si
ahora tomamos la tabla del número de individuos infectados en Bogotá[4] y ajustamos los parámetros
de la función de Gompertz en forma conveniente obtenemos el siguiente gráfico:
Gráfico 5: Modelo de Gompertz
Que
muestra un ajuste bastante cercano entre los individuos afectados en el período
6 marzo a 5 de mayo, pero a su vez permite por Gompertz llevar a cabo una
proyección que en este caso iría hasta el 17 de junio y que daría para esa
fecha un total de 4.771 infectados.
Quizás
uno de los modelos más utilizados es el modelo de compartimentos SIR (Susceptibles–Infectados-Removidos[6]). Este modelo
epidemiológico desarrollado por Kermack&McKendrick en 1927 relaciona las
tres variables en cuestión – S, I y R – por medio de un sistema de ecuaciones
diferenciales, pero el caso que se va tratar aquí se introduce un nuevo
compartimento llamado E (Expuestos) que son personas que están infectadas pero
no han presentado síntomas del COVID-19. Es decir, se tiene un modelo tipo
SEIR:
Las
respectivas ecuaciones diferenciales tienen la forma:
Donde ß, llamado tasa de transmisión, de
manera que 1/ß mide la probabilidad
de que un susceptible se infecte cuando entra en contacto con un infectado y ƴ, llamado tasa de recuperación, de
manera que el periodo medio de recuperación es 1/ƴ. Se introduce un nuevo compartimento llamado E (Expuestos) y σ,
de forma tal que 1/σ es el tiempo promedio de incubación. Nótese que
para ambos casos se tiene:
SIR:
S+I+R = N y para el SEIR: S+E+I+R = N
Tomando
en forma discreta las ecuaciones del modelo SEIR y tomando un período de
observación que va hasta el 31 de diciembre del 2020 se tiene el siguiente
resultado para Bogotá:
Gráfico 6: Modelo y Observaciones reales
marzo-mayo de 2020
Aquí no se detecta ningún ‘aplanamiento’. El modelo se ajusta
por medio de la elección de los parámetros. En particular los valores de Ro (R sub cero) van variando
desde 3.1 a 2.0.
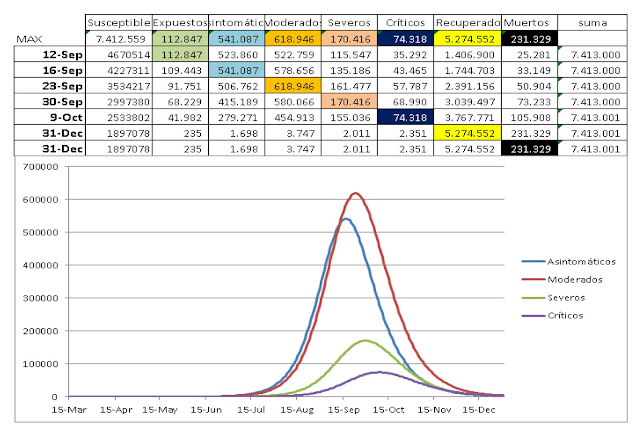
Grafico 7: Proyección
Infectados y Expuestos por el modelo
Fuente: vea Gráfico 6
El modelo muestra la proyección hasta diciembre 31 de 2020
llegando a tener para esa época un total de 340.572 con un máximo de 880.635 el
28 de octubre de 2020.
En el mismo sentido se observa la proyección de los casos
Susceptibles y Expuestos:
Gráfico 8: Proyección
Expuestos y Susceptibles
Fuente: vea Gráfico 6
Conclusión:
Con base en el modelo expuesto, que no es exacto debido a que
en el tiempo los parámetros se van ajustando y se va calibrando el modelo y que
se pierde precisión al tomar la versión discreta, sí deja ver que el virus no
se acabará pronto.
Por último, se presenta el modelo desarrollado para Bogotá, por un grupo
de investigadores que parte de la misma filosofía del modelo básico SIR.
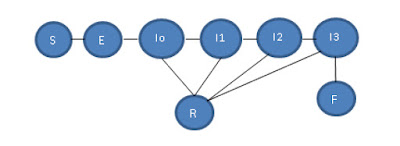
Modelo SEIRF para Bogotá
Este modelo amplia el
modelo SIR al introducir un conjunto de nuevos compartimentos. El modelo fue desarrollado
por Juan Diego Mejía Becerra (Secretaría Distrital de Salud de Bogotá) Revisión
de Zulma M. Cucunubá (Imperial College Londres), Fernando de la Hoz Restrepo
(Universidad Nacional de Colombia), Darío Londoño Trujillo (Universidad de los
Andes) y Diane Moyano Romero (Secretaría de Salud de Bogotá)[7] El esquema del modelo es
ahora:
donde los
compartimentos en los cuales se divide la población son:
- Susceptibles(S): Aquellos individuos que no han sido expuestos al virus y son susceptibles a ser infectados.
- Expuestos(E): Aquellos individuos que se encuentran en el período de latencia. Han sido inoculados por el patógeno pero aún no son infecciosos.
- Infecciosos Asintomáticos(Io): individuos que han sido inoculados por el virus son infecciosos, pero no han desarrollado síntomas.
- Infecciosos con síntomas Moderados(I1): infecciosos que presentan síntomas leves. Están en la casa, por lo general.
- Infecciosos con síntomas Severos(I2): presentan síntomas severos, pero no críticos. Requieren hospitalización.
- Infecciosos críticos(I3): presentan síntomas críticos. Requieren atención en UCI.
- Recuperados(R): pacientes que se recuperaron y no se vuelven a infectar.
- Muertos(F): individuos que fallecen a causa del virus.
El modelo se rige por
un conjunto de ecuaciones diferenciales que relacionan las anteriores
variables:
Los parámetros ßi, ωi, δi,
ƴi, σi son determinantes en la evolución del sistema. Nótese,
en particular que ß0 y ß1 no son fijos como los otros sino dependen del
tiempo. Precisamente esta propiedad hace que el trabajo presente tres
escenarios que son:
· Escenario 1 básico sin ninguna
intervención
· Escenario 2 con cuarentena hasta 27 de
abril
· Escenario 3 con cuarentena hasta 20 de
junio
Es supremamente
ilustrativo poder observar cómo se modifican las curvas respectivas de los
Infectados:
Escenario1: sin restricciones
Escenario2: cuarentena hasta 27 abril
Escenario 3: cuarentena hasta 30 de junio
En primer lugar,
nótese como se van corriendo en el tiempo los picos de las curvas.
En segundo lugar,
para los escenarios 2 y 3, todos los parámetros se dejan iguales excepto ß0(t) y ß1(t) que recogen las características de los escenarios.
En tercer lugar,
nótese que los valores máximos son para los escenarios 2 y 3 casi iguales con
la sola diferencia de que en el primer caso los picos están en julio/agosto
mientras que en el escenario 3 en septiembre/octubre.
Finalmente cabe
observar en el siguiente gráfico que sucede en los 3 escenarios descritos con el
número reproductivo efectivo Rt (R sub–t), que es función del número
reproductivo básico R0 (R sub-cero), pero que va variando con el
tiempo.
Lo notorio son los
saltos del valor del número reproductivo en los momentos en los cuales se
termina la cuarentena -26 abril en el escenario 2 y 30 junio en el escenario 3-
Consideraciones finales
Es indudable la
bondad del modelo para Bogotá. Es más completo que los otros y permite por
medio de cambiar el valor de los parámetros hacer ajustes a medida que se va
avanzando en el tiempo. Es decir, es relativamente fácil actualizarlo. Se
incluyó el modelo SIR dado su carácter de pionero y precisamente el modelo de
Bogotá es una variante con la misma filosofía. En la literatura sobre el tema
hay modelos donde se incluye adicionalmente ecuaciones que recogen la dinámica
de nacimientos y defunciones por otras causas u otras variables. Sin embargo,
en la mayoría de casos se trata de esquemas de compartimentos.
Finalmente, es importante
resaltar que la comunidad científica ha desarrollado y publicado muchos otros
modelos entre los cuales están, para sólo mencionar algunos, el modelo del
Imperial College de Londres[8], los modelos de la
Universidad de Laguna en Tenerife(España)[9] o el estudio de la
Universidad Politécnica de Valencia[10].
Un
caso que llamó mucho la atención es el documento: When will Covid-19 end? Data-driven Prediction.[11] Esto se debe a que de
nuevo utilizando un modelo tipo SIR predice para muchos países del mundo cuando
se va a terminar el virus. Aunque es interesante, no deja de tener un pero muy
importante que consiste en anunciar el fin de la historia y precisamente este
punto se contradice por muchos de los otros modelos expuestos o nombrados en
este documento.
Nota final
Al
momento de escribir este documento, es alarmante la evolución de infectados en
la localidad de Kennedy en Bogotá: para este mes de mayo los números publicados
en la página de Bogotá: https://bogota.gov.co/coronavirus-en-bogota/
muestran una secuencia de nuevos infectados de 9-18-27-22-51-50-51, es decir
186 nuevos casos del total de 719 (25.9%) en sete días.
[2] Se calcula con base en:
donde a es la amplitud
(No. de días) y los Y son los valores acumulados desde el inicio i hasta el final
t.
[4] De nuevo de datos https://bogota.gov.co/coronavirus-en-bogota/
[5] W. O. Kermack & A. G.
McKendrick "A contribution to the mathematical theory of
epidemics" Proceedings of the Royal Society of London Series A,
115:700-721, 1927
[6] Se utiliza Removidos en cambio de lo
que se utiliza interpretando la R como Recuperados porque se incluyen aquí
tantos éstos como los fallecidos.
[7] Modelación Matemática
de la Propagación del SARS-CoV-2 en la Ciudad de Bogotá, Segunda Versión,
Bogotá, abril 4 de 2020. De nuevo en: http://saludata.saludcapital.gov.co/osb/wp-content/uploads/2020/04/Ficha_Metodologica.pdf
[11]
Jianxi Luo Data-Driven Innovation Lab
(http://ddi.sutd.edu.sg) Singapore University of Technology and Design (http://www.sutd.edu.sg)
EmoticonEmoticon